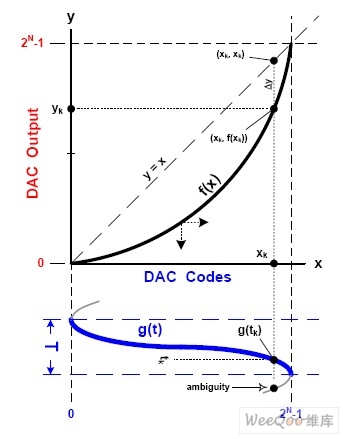
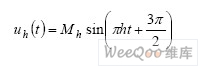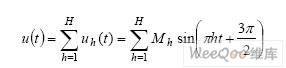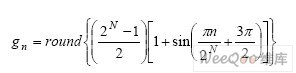дҝ®ж”№/еҲӘйҷӨйҮҮиіј
委жүҳеҜ� | жң�(huГ¬)е“ЎжңҚеӢ�(wГ№) иӘ�(rГЁn)иӯүжңҚеӢ�(wГ№)

еҹәзӨҺ(chЗ”)жң�(huГ¬)е“ЎжңҚеӢ�(wГ№)
зҷҫз¶ӯйҖ�
и»ҹж–ҮзҮҹйҠ· | е·ҘзЁӢеё«жңҚеӢ�(wГ№) PDFдёӢијү
жҠҖиЎ�(shГ№)иіҮж–ҷ
йӣ»еӯҗиіҮиЁҠ
йӣ»и·Ҝең� | з¶�(wЗҺng)з«ҷе°Һ(dЗҺo)иҲ� з¶�(wЗҺng)з«ҷйҰ–й �
йӣ»еӯҗе…ғеҷЁд»�
ICдәӨжҳ“з¶�(wЗҺng)
жҠҖиЎ�(shГ№)иіҮж–ҷ
йӣ»еӯҗиіҮиЁҠ
Datasheet
йӣ»и·Ҝең�
йӣ»еӯҗйҖ�